
Transformers in Real Life: Shape Memory Alloys or Revolutionary Properties in Science and the Game Changer in Industry
Fascinated by the sci-fi movie Transformers? The alien robots in those films disguise themselves as normal vehicles, switching back and forth at will between their forms as either inconspicuous machinery or powerful, giant fighters. This switching, bending and reshaping of metal does seem quite a sci-fi concept for anyone who has ever bent a spoon, or any metal piece out of shape and tried to return it to its original form. It simply never goes back to the way it was before!
However, this sort of metal being able to change its form and return to its original shape actually does exist! These new metals, a unique class of alloys (a metal made by mixing together two or more metals with other substances) are called Shape Memory Alloys (SMAs), and like the Transformers in the movies are able to undergo ‘transformation,’ where the metal can remember, recover, and even return to its original shape after being bent or twisted.
Shape Memory Alloys –
Special Properties Make Them Revolutionary
Recoverability
The magic behind SMAs is attributed to the so called “Martensitic Transformation”. This transformation is a process in which symmetrical crystals (called austensitic crystals) can turn into low-symmetry crystals (called martensic crytals), and vice versa. A “Martensic Transformation” is one characterized by these two phases. With this transformation also comes a shape change, which leads us back to the Transformers aspect of Shape Memory Alloys!

This recoverability of SMAs is what makes them revolutionary, especially when compared to other conventional metals (just think of the spoon you are using daily!). After being deformed, SMAs are able to recover up to 8% of the induced strain without significant residual strains, whereas for conventional metals or alloys, for example steel, the recoverable strain is an order of 0.1%.
High Power to Weight Ratio
Besides their ability to return to their former shape, the high power to weight ratio (PWR) is another outstanding feature of Shape Memory Alloys. Let’s take a short look at this.
To put it in a nutshell, plants’ potential of adapting to various environmental conditions is insufficiently understood, especially with regard to crop breeding. This is where Anna’s research comes in: Understanding the plants’ mechanisms of environmental monitoring and acclimation is of fundamental importance if we are to transition to a sustainable agriculture that will also be fundamental to a climate friendly bioeconomy.
What is the value of a high PWR? Well, as a first example we can think about aeronautics. It is more cost-effective to send to the sky a transducer (e.g. actuator, motor, etc.) which can produce more power but with less weight…imagine you are an astronaut going to the moon to collect moon stones; for breaking the rocks you need to choose the right tools – let‘s assume the decision is between a DC motor (PWR ~1 W/kg) and an SMA actuator (PWR ~100 W/kg). For your mission, you need a 60W transducer (which has the same power as your old bedroom lamp, by the way), so let’s do some simple arithmetic: based solely off Power to Weight ratios, you must choose between an SMA actuator of 0.6kg and a DC motor of 60kg. I hope you would make a good choice which could satisfy your rocket designer, since they should be the most concerned with your rocket’s payload 🙂
In NASA’s case, they use SMA-Actuated Rock Splitters (SMARS for short) when dealing with planetary bodies such as the Moon, Mars, and near-Earth asteroids.
After heating up, the SMA can eventually exert up to 1500 MPa of stress, swiftly splitting the rock apart. The significant advantages are as follows: firstly, it is much more cost-effective, and secondly, it is considered the more environmentally-friendly method for splitting apart rock formations in a controlled manner, able to get the job done without the use of explosives or hydraulics.

Research on Shape Memory Alloys: Reaching the Peak of Perfection or Making the Unknown Known
Despite all the features that made SMAs appealing to industrial and scientific worlds, there are still many efforts to be made in order to make them more suitable and reliable for use in different domains of application.
The Mysteries Behind Martensitic Transformation

As mentioned above, the properties of SMAs such as their recoverability have made them a revolutionary alloy.
But to be honest, this recoverability is not perfect! In fact, after thermomechanical loading, the SMAs cannot 100% fully recover from the deformation they have been through. We call the extent to which an SMA can’t recover its “unrecoverability”. There are still various mysteries linked to this measurement.
What makes SMAs unrecoverable is as crucial as their recoverability: only if we fully understand the unrecoverability, we will be able to improve the recoverability. SMAs’ unrecoverability, when subjected to thermo mechanical loadings, are mostly related to their microstructure defects such as twinning, dislocation, and misorientation. In research, microstructural features such as these have been studied for a long time in crystallography, which is the experimental science of determining the arrangement of atoms in crystalline solids. So are you ready to knock open the door of crystallography?
Taking a Deep Dive Into the Inner Structure of a Diamond – How Crystallography Helps Us Understand the Recoverability Features of SMAs
You all know emeralds or diamonds. These precious stones are mineral crystals whose atoms are highly arranged in a periodic order. This arrangement is also found in metals and alloys, hence they are also crystals. To better understand the internal structure of such materials, it is best to imagine a great many Rubik’s cubes neatly stacked – as in this picture:

© WiRe / Studio Sonnewald
The stack of cubes is basically structured like the inside of a crystal – where a cube is a “unit cell” of the crystal.
Now it’s important to note we are looking at a three-dimensional structure here from a very specific point of view.
We can further imagine that we transfer this structure into a three-dimensional coordinate system.
If we now assume that a cube, a “unit cell” of the crystal, has a certain height, length and width, say 100mm each, we can use the coordinate system to determine, for example, the coordinates of the corners of the cube facing us.
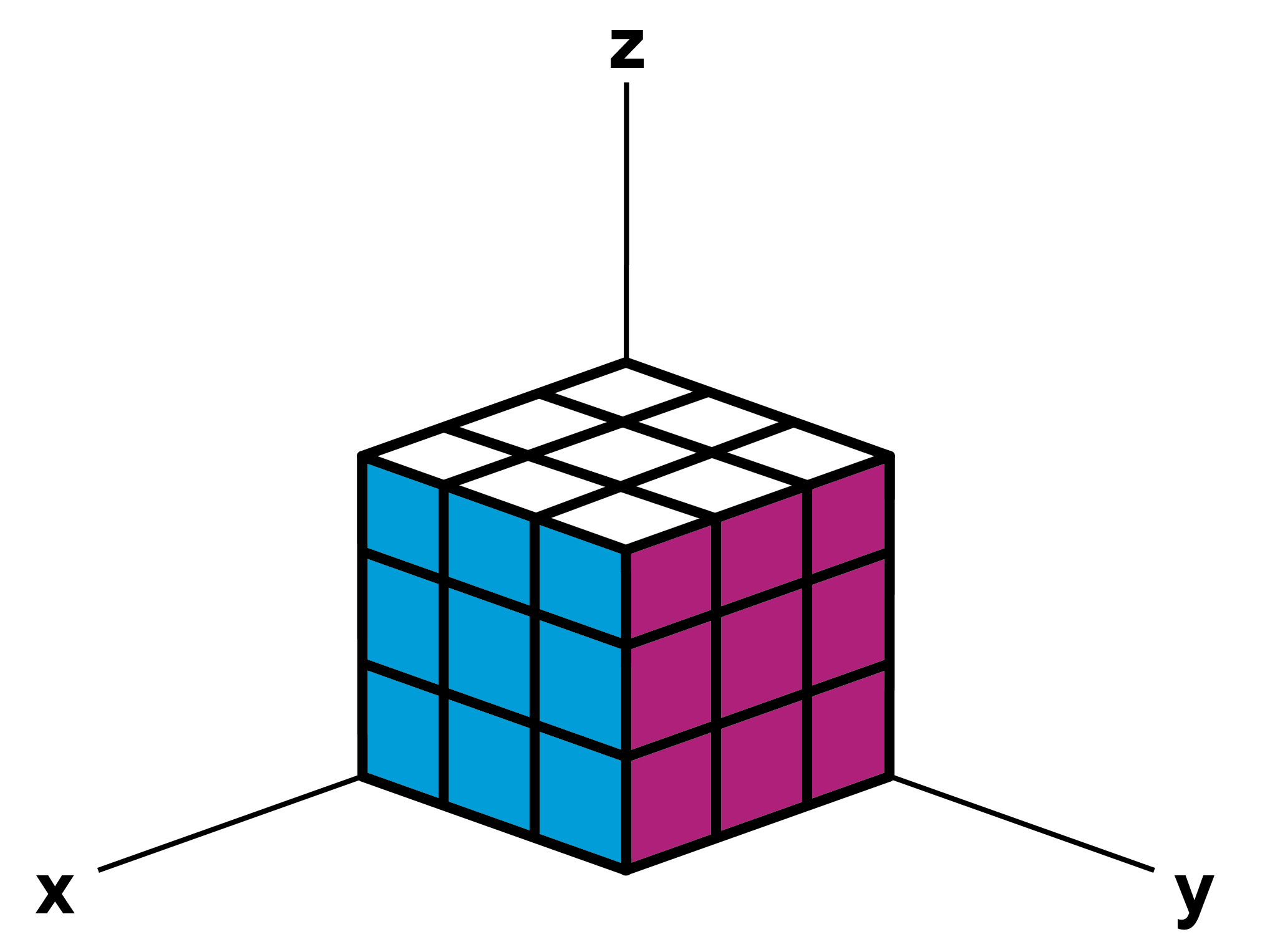
© WiRe / Studio Sonnewald

Directions: X: [100] / Y: [010] / Z:[001]
© WiRe / Studio Sonnewald
In crystallography we use the same philosophy to describe crystal orientations. The coordinate system we use is called Miller indices. For example, let’s take an austenic NiTi unit cell (which is also a cube) and mark it with Miller indices, as shown in the image below. With the Miller indices, we can intentionally “look at” and “rotate” crystals (as with a Rubik’s cube) without having difficulty determining the “line of sight” and the “directions”:
Taking a Deeper Look Into Disorder – or the Structure of Polycrystallines
In practice, polycrystals are more widely used than single crystals because they have higher strength and lower production costs. Therefore, polycrystalline SMAs are used for most SMA applications. So what is the difference between single crystal and polycrystalline structures? Let’s go back to our Rubik’s Cubes – but this time, let’s imagine that they were not stacked as perfectly as in the picture above:

© WiRe / Studio Sonnewald

© WiRe / Studio Sonnewald
Unlike last time, here we don’t have all the cubes aligned the same way. Rather, here we have groups of cubes arranged in the same way, with each group (e.g. one Rubik’s cube) “facing” in a different direction. And so we have the structure of a polycrystal – a group corresponds to a “grain” of a polycrystal and the groups are the boundaries between the grains! If we now color the different groups, we get this picture:
How These “Disordered” Microstructures Come Into Being
As mentioned earlier, the Miller indices make it easier to determine grain orientation and rotation. This is useful because the individual grains of a polycrystal – or an SMA – can “suddenly rotate” during thermomechanical loading. This happens, for example, when a certain stress-strain temperature threshold is reached.
For example, under mechanical loading, randomly oriented grains (e.g., figure above) in austenitic polycrystalline NiTi SMA wire tend to rotate along the axial axis (wire axis) into a [1 1 1] orientation, as shown in the Figure below. If one increases the mechanical load, massive defects are introduced into the structure. These lead to the fact that the original structure cannot be restored.
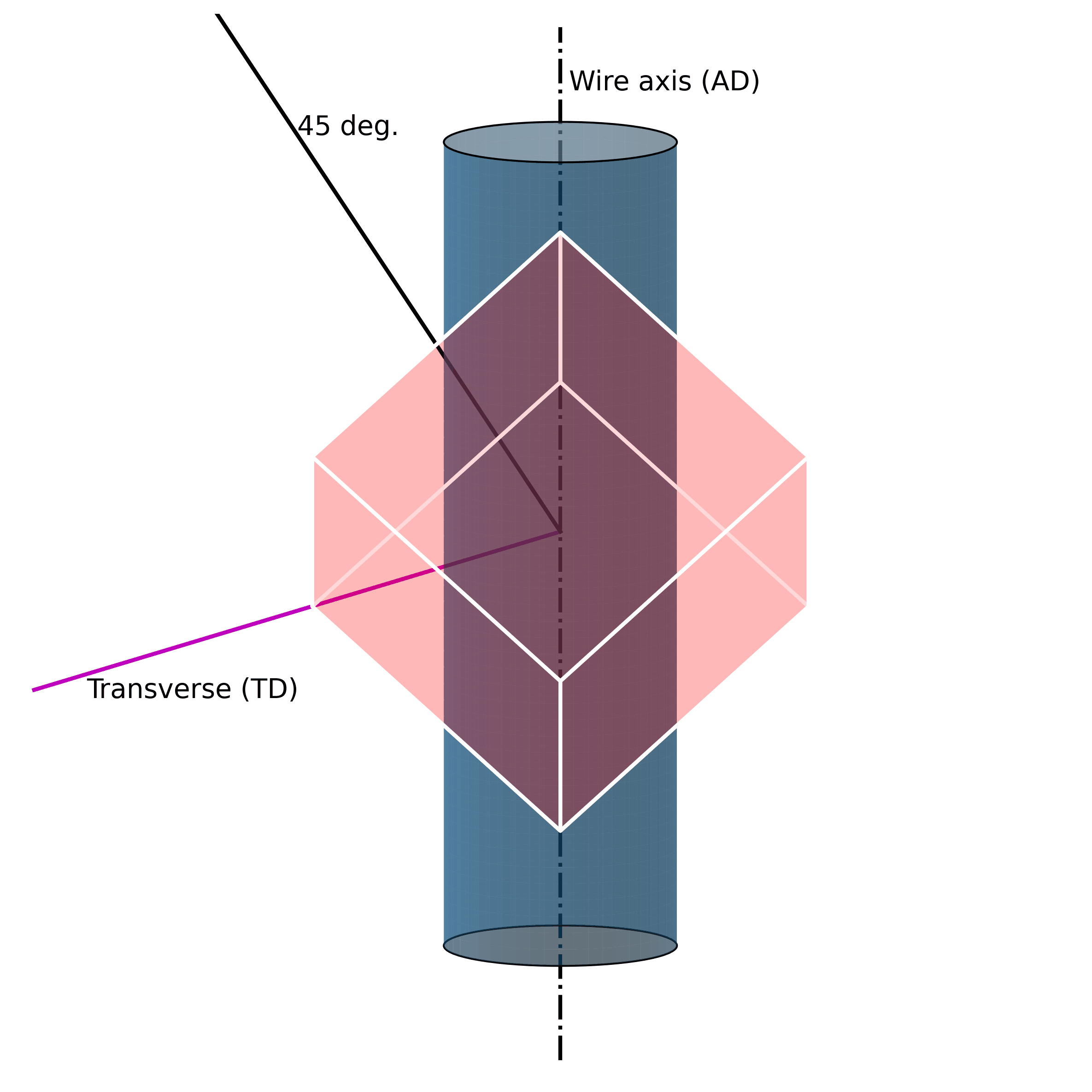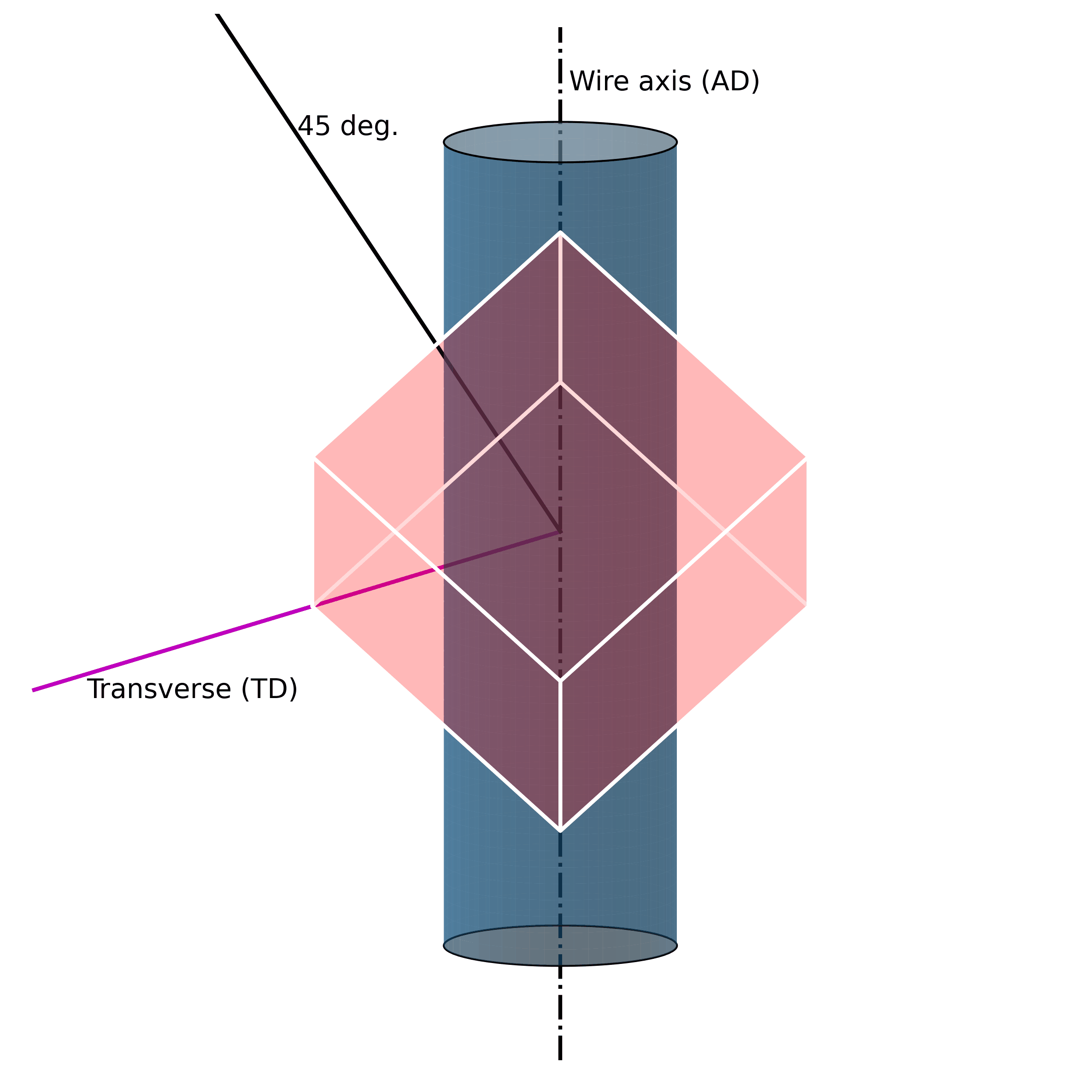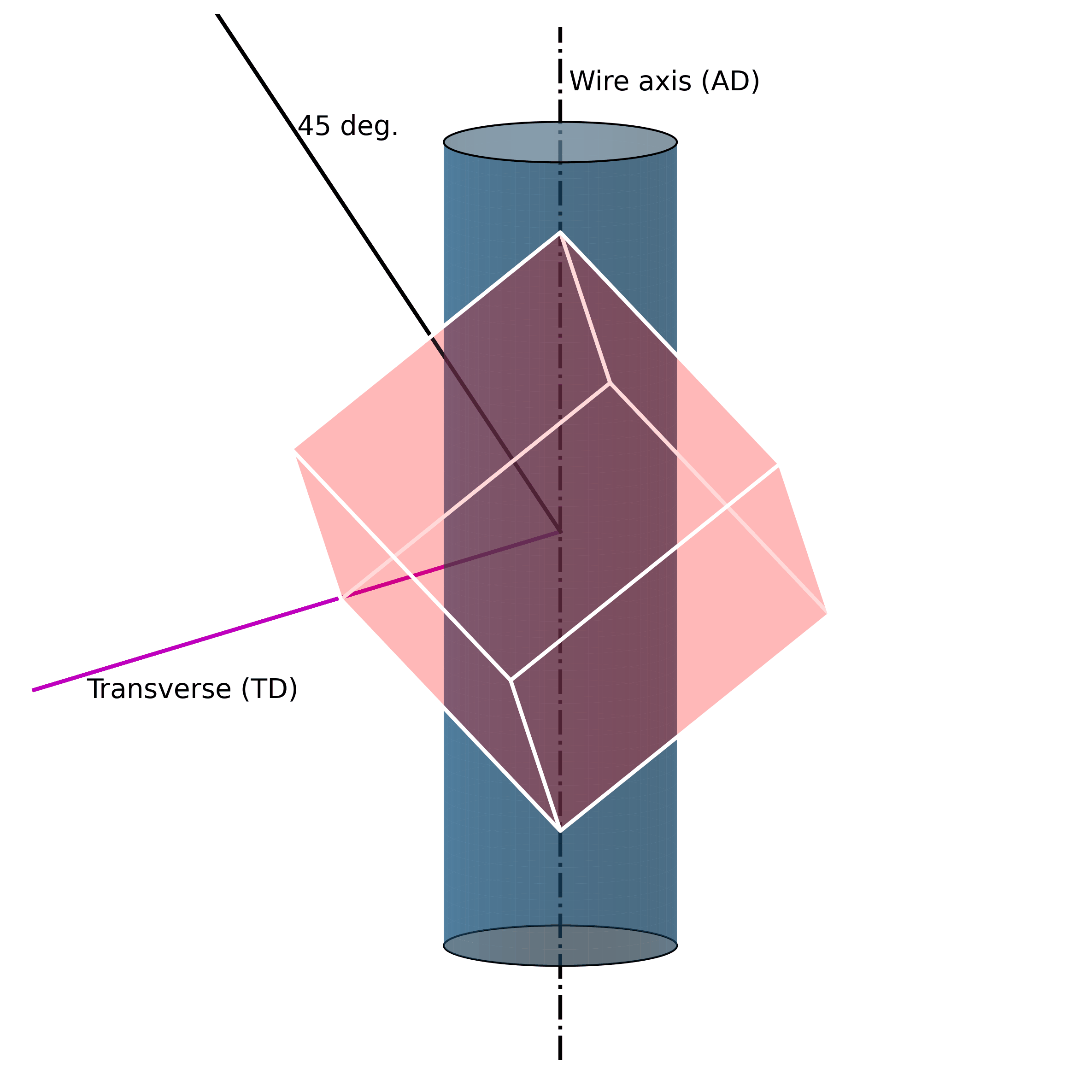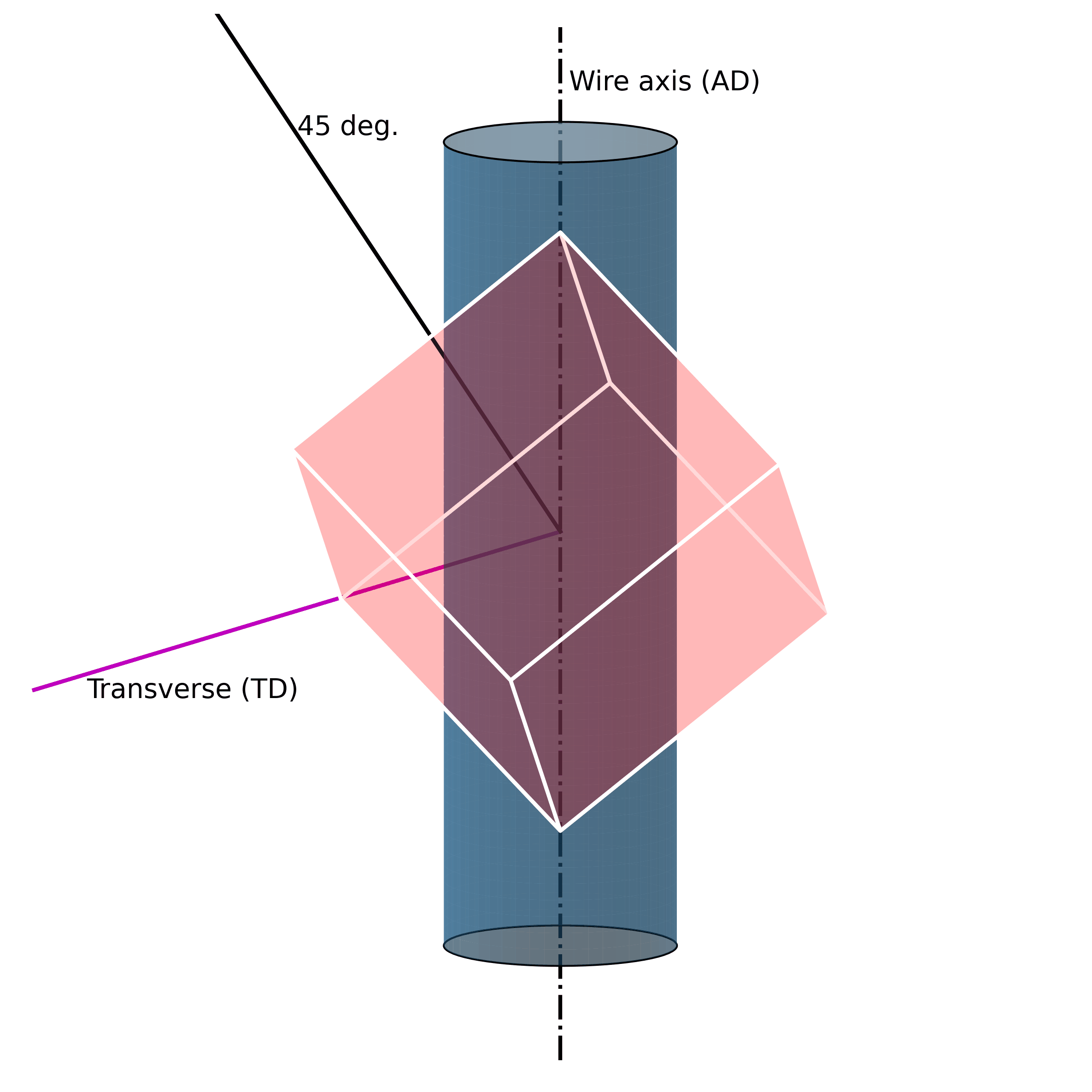
Such microstructural defects (such as twinning, dislocations, and misorientations) are thus the reason for the unrecoverability of SMAs. They are the key to unlocking the secrets of unrecoverability. We now know that such defects in the microstructure allow SMAs to exhibit large strains without breaking. However, because they are “defects“ of their structure, they simultaneously impair their ability to return to their original shape.
Further research into such changes in the microstructure of SMAs will allow us to produce even better SMAs, which can then be used in further engineering and scientific applications.
Acknowledgements:
The author would like to thank Dr. Luděk Heller and Dr. Wei Li very much for their kind help on image creation.
