
How Can Mathematics Help To Reduce Confusion In Information Transmission?
Have you ever been curious about what mathematical research looks like, or wondered how abstract mathematics is applied in real life? Let me take you on an exciting journey to answer questions about how mathematics is helping to develop the next generation of information technology. We will take a short trip through the fascinating world of Quantum Information Theory (QIT) and discover its deep ties to mathematics. Along the way, I will give you an insight into my research in mathematics by exploring concepts like quantum graphs and the role of operator algebras. So buckle up and let’s dive in!
Quantum Information Theory: The Next Generation of Information Technology
Quantum science generally refers to the study of the smallest particles of matter and energy. Quantum information theory (QIT) is the science of processing and transmitting information using the principles of quantum science in ways that cannot be achieved using the principles of classic physics.
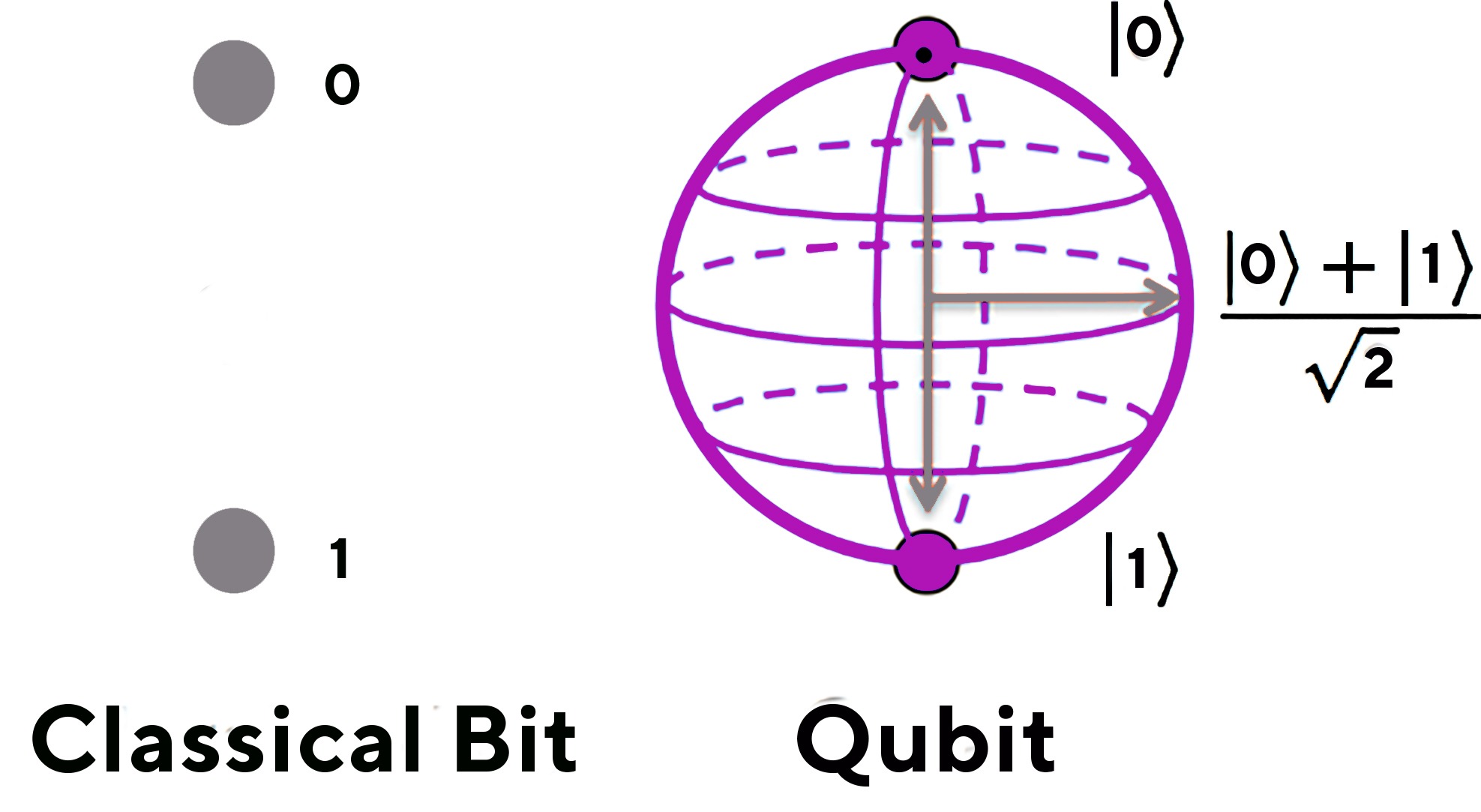
So, how are quantum principles different from classical principles ? In classical technology (such as our computers and smartphones), information is processed using “bits” which can only take one of two possible values, usually denoted by a 0 or a 1. In quantum information theory, we use quantum bits or “qubits” instead.
Qubits represent the state of quantum systems (e.g. the spin of an electron) and can be either 0 or 1, or both at the same time through a property called “superposition”. Qubits can also be “entangled”, so that the state of one depends on the state of the other, even if they are hundreds of miles apart! Superposition and entanglement are unique features of the quantum world that do not exist in the classical world.
These special properties allow quantum systems to process information in unparalleled ways!

The Link Between Mathematics and Quantum Information Theory
Mathematics provides the language and tools required to describe the behaviour of quantum systems. For instance, qubits are represented by vectors and the superposition property is expressed by linear combinations.
From linear algebra to probability theory, various fields of mathematics play a key role in quantum information theory. The synergy between quantum information theory and mathematics has historically led to breakthroughs in both fields, highlighting their symbiotic relationship. In particular, “operator algebra” is a branch of mathematics that provides a robust framework for studying and describing quantum phenomena. Let’s explore what operator algebra is!
Operator Algebra: The Quantum Framework
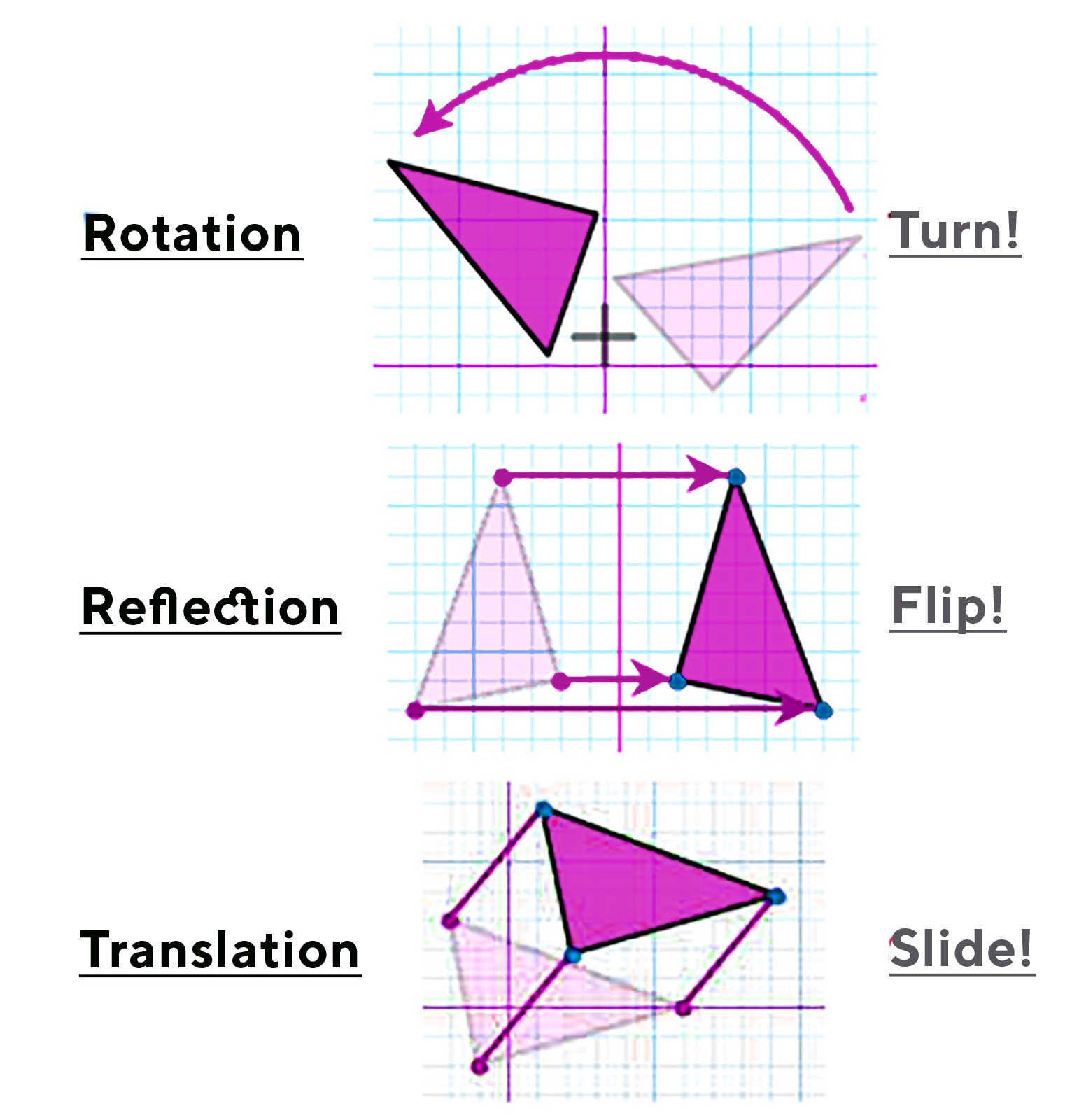
Imagine you have a rubber band with some marks on it at equal distances. If you stretch the rubber band, the distance between the marks will increase. But you can verify that the marks are still equally spaced . The stretching operation basically transforms the rubber band in a uniform way so that its mark structure is preserved. In mathematics, such transformations are described by (linear) operators.
An operator is like a machine that takes an object, performs an operation on it, and returns a new object. Operators have some special properties so that they are able to “preserve” the structure of the original object. In the finite dimensional setting (such as our three dimensional world), operators are represented by matrices. Common examples of operators are expansions (stretching/shrinking), rotations, reflections (inverting) and translations (shifting). By applying a combination of operators to basic shapes (like triangles and circles), we can create complex shapes. This is commonly used to generate computer graphics and animated scenes.
To put it in a nutshell: Operator algebra is the study of collections of operators on linear spaces, including infinite dimensional vector spaces. Operator algebraic tools are very useful in quantum information theory, where quantum states are represented by vectors and their evolution is described by operators.
The Role of Operators in Information Transmission
Did you know that we also use operators for communication every day? When we send information through a channel, like sending a text message, it is implemented by an operator that takes inputs as alphabets and produces output alphabets. Similarly, in quantum information theory, the transmission of information is achieved using an operator called “quantum channel”, which takes one quantum state to another.
By understanding the mathematical properties of these operators, we can achieve more efficient and secure transmission of information. This is what my research does! Let’s discuss this in a little more detail.
Noisy Communication and Confusability Graphs
Have you ever confused two words in a phone conversation? Communication channels are often imperfect and subject to noise, which distorts the information being transmitted. For instance, a receiver may be confused between words like “nice” and “rice” as they sound similar. The likelihood that two messages may be confused with one another in a channel can be modeled using a diagram of nodes and edges called a “confusability graph” (Figure 4). The nodes of a confusability graph represent the input messages transmitted through the channel, and the edges represent messages that can be confused with one another in the course of transmission. The more connections we have between the nodes in the confusability graph, the higher the level of confusion in the channel.

The confusability graph of Φ is given on the right. © Dr. Priyanga Ganesan
Quantum Graphs: My WiRe Research Project
Confusion may also occur while sending information through a quantum channel. To model the confusion in this case, we need more sophisticated mathematical objects called “quantum graphs”. A quantum graph is a special collection of operators (a structure known as an “operator system”) that plays the role of a confusability graph in quantum information theory. By understanding the mathematical properties of quantum graphs, we can develop accurate transmission of messages through a quantum channel.
My research broadly investigates the mathematical structure of quantum graphs using tools from operator algebra. For my WiRe research project at the Cluster of Excellence Mathematics Münster, I am particularly focused on a geometric feature of quantum graphs called “connectivity”, which measures the noise in the quantum channel.
Broader Implications
You may be wondering, “All this is interesting, but how does it affect me?”
The advancements in quantum information theory are setting the stage for ground-breaking technologies. One example of this is quantum computing. Quantum computers, which are on the horizon, have unmatched power in code-breaking and can break current security systems that we use every day! For instance, many of the current encryption algorithms that are used to protect sensitive information (such as credit card purchases) are based on the difficulty of factoring large numbers. This can be easily solved by a quantum computer, thanks to the use of qubits! Quantum computing promises to tackle problems that are beyond the reach of classical computing, and in return will help us develop more secure cryptographic systems.

Quantum Information Theory in the Future
Quantum information theory, with its rich mathematical underpinnings, is paving the way for the next generation of technologies. It has the potential to revolutionize the world by solving problems and finding solutions that we are currently unable to achieve. However, we are still far away from implementing it in practice and we need more understanding of the intricacies involved in the process. Mathematical research will be our guiding light as we continue to dive deep into this endeavour.
As the world is rapidly advancing in this direction, maybe within 20 years from now we might all be using new computers and self-driving cars powered by quantum technology!
